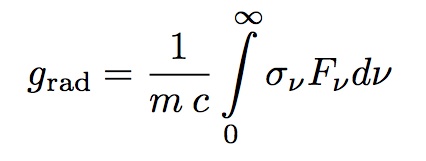

Radiative acceleration (sometimes called radiation force) is an important ingredient for the evaluation of the diffusion velocity. The acceleration on a given species is due to the momentum acquired by atoms from the radiation field during photoexcitation or photoionization. The value of the radiative acceleration of a species depends on its absorption cross-section, its local concentration and the local radiation flux. The radiative acceleration due to bound-bound transitions is generally larger than the acceleration due to bound-free transitions.
A generic expression for the radiative acceleration grad of a given atom at a given depth can be evaluated using the following equation in a plane-parallel approximation (see also Michaud 1970):
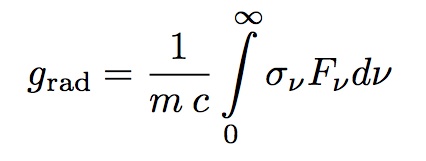
where Fνdν is the net outward radiation flux in the frequency range dν, σν is the monochromatic absorption cross-section of the species under consideration, m and c are the mass of the atom and the velocity of light.
It should be noted that radiative acceleration (or radiation force) is different from radiation pressure. Indeed, radiative acceleration is a vector oriented in the same direction as the radiation net flux, while radiation pressure is a scalar measuring the pressure of the photon gas (all photons). Rigorously speaking, radiative accelerations are weighted sum of the gradients of partial radiation pressures (for each species). Radiative acceleration grad has a statistical meaning: it is an average over a huge number of microscopic interactions with photons in all directions. It represents the average momentum acquired by a single atom from the radiation field and it is usually expressed in cm.s-2.
In stellar modeling, radiative accelerations have to be computed for each species and even for each type of ion existing in the medium according to their detailed absorption cross-sections. Such detailed calculations require considerable computing power and necessitate the access to large atomic databases. Actually, in concrete computations, the simple expression shown above is not enough to account for the complexity of the physical processes involved by the momentum transfer from photons to atoms (as for instance the redistribution of momentum among the ions of a given chemical element). In most cases, grad is a vector having the same direction as the net outward radiation flux. This is not the case in magnetic fields because of (i) the Zeeman effect (the equations of polarized radiation transfer have to be solved in non plane-parallel case), and of (ii) the contribution of photoionization to the radiative acceleration due to the momentum partly given to ejected electrons. Detailed presentations and discussions can be found in the following references:
According to specific modeling needs, and besides the numerically accurate methods (but requiring large computing ressources), there are several possible approximations such as the SVP approximation presented on this web site.
An example of the radiative acceleration of scandium in an A-type star is shown in the figure below. Two dips at depths where scandium is found in a noble gas configuration (i.e. Ar-like and Ne-like configurations) are seen on this figure because such ions have a weak opacity spectrum and therefore absorb a lesser amount of photons.
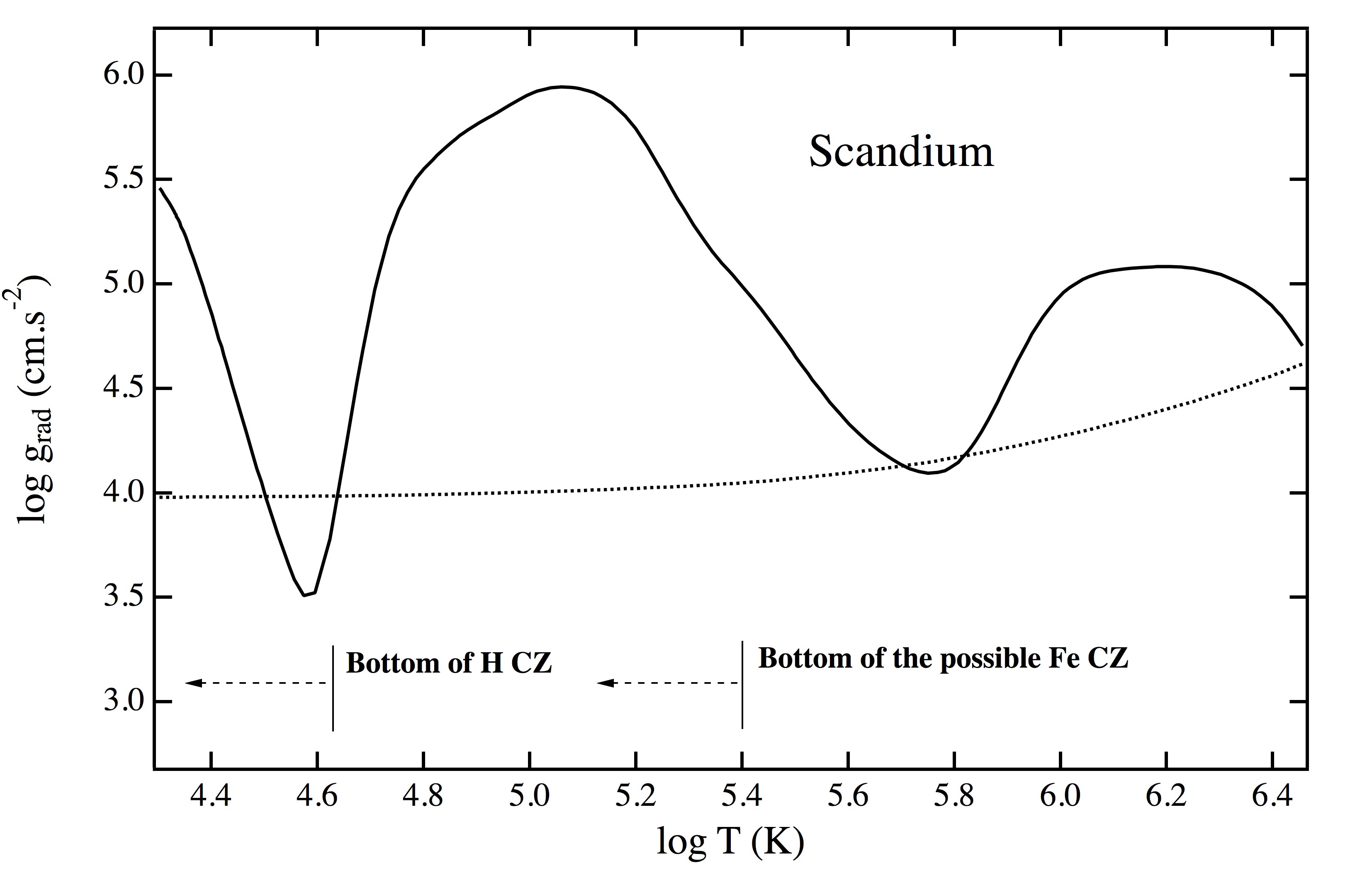
Radiative acceleration of Sc for a solar abundance vs. the depth (temperature T is in K) in a star with Teff = 7610 K (for an Am star). The solid line corresponds to the radiative acceleration using the SVP method. The approximate locations of the bottom of the convection zones due to H ionization and to iron overabundance (predicted by Richer et al. 2000) are shown. The dotted line represents the local gravity. For more details about the diffusion of Sc in Am stars see Alecian et al. 2013.